背包问题的贪心算法：局部最优，全局高效

背包问题是一个经典的组合优化问题，常常在算法设计与分析中被提及。而背包问题的贪心选择性质则是解决该问题的一种有效策略。通过对物品的价值和重量进行比较，选择具有最大单位价值的物品放入背包，可以得到近似最优解。

贪心算法是一种基于局部最优选择的策略，在背包问题中也同样适用。其核心思想是每次都选择当前具有最大单位价值的物品放入背包，直至背包无法再容纳更多物品或者所有物品都已经考虑完毕。

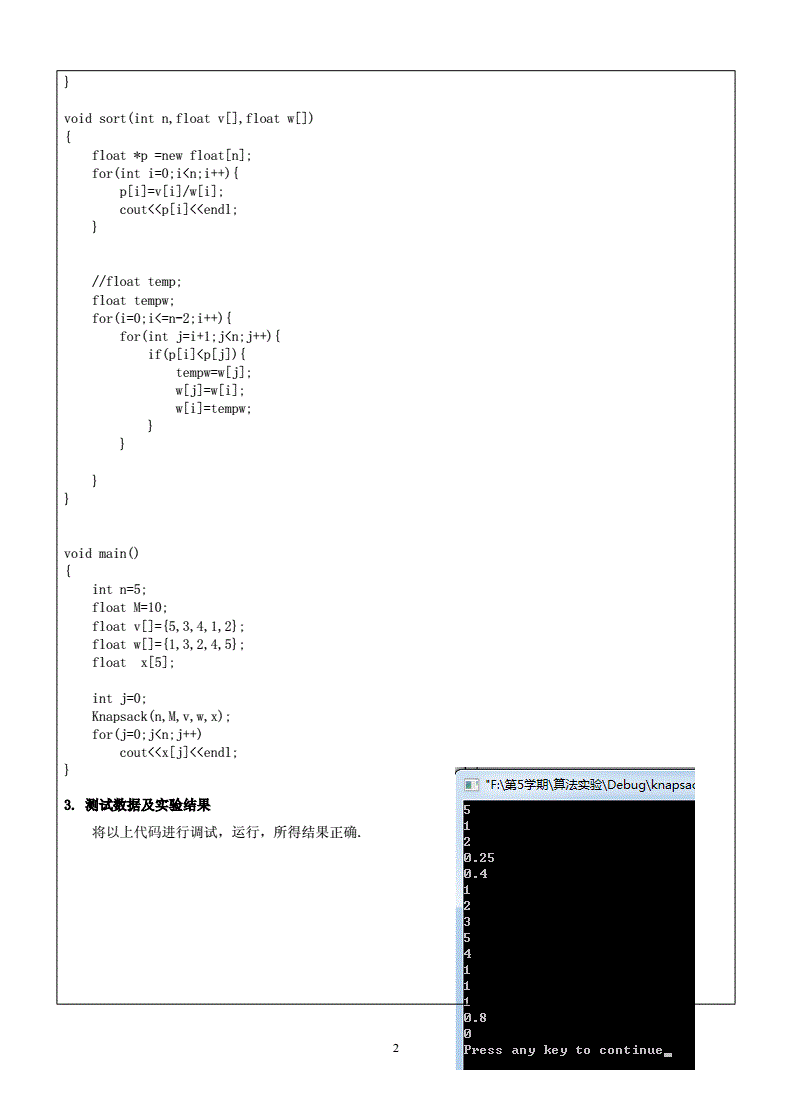
这种贪心选择性质的好处在于它能够快速得到一个可行解，并且在某些情况下能够接近最优解。因为该策略保证了每次都选择当前最优的物品，所以在一些特殊情况下，贪心算法能够得到全局最优解。

然而，需要注意的是，并非所有背包问题都适用于贪心选择性质。当物品之间存在相互制约关系或者限制条件时，贪心算法可能无法得到最优解。此时，需要采用其他更为复杂的算法来求解背包问题。

总而言之，背包问题的贪心选择性质是一种简单而有效的解决方案。通过选择具有最大单位价值的物品放入背包，可以得到近似最优解。然而，在实际应用中需要根据具体情况选择合适的算法来解决背包问题。